

 |
 |
 |
  |
|||||
| המדריך השלם | |||||
|
|
|
עצים בינאריים
עץ בינארי - מבנה נתונים מופשט הבנוי הצורה הפוכה לעץ טבעי כלומר שורשו למעלה והסתעפותו כלפי מטה, כך שבתחתית מצויים ענפיו ועליו. הצומת העליון הוא שורש העץ. כל נקודת הסתעפות נקראת צומת ולכל צומת שני ענפים, שמאלי וימני (במקרה של עץ בינארי). שני צמתים של ענפים אלו נקראים בנים או ילדים (ימני ושמאלי) של צומת ההסתעפות וצומת ההסתעפות נקרא אב של שני בנים אלו.  הערה: העץ נקרא בינארי מכיוון שלכל צומת יש לכל היותר שני בנים. ניתן לייצר גם עצים תרינאריים ויותר על ידי הגדלת מספר הבנים לכל צומת. הערה: העץ נקרא בינארי מכיוון שלכל צומת יש לכל היותר שני בנים. ניתן לייצר גם עצים תרינאריים ויותר על ידי הגדלת מספר הבנים לכל צומת.כל צומת מהווה גם היא שורש של תת עץ (עץ נתונים הוא בעל דמיון עצמי מושלם). לכל צומת יש הורה אחד בלבד. עלה הוא צומת שאין לו ילדים, צומת פנימי הוא צומת שאינו עלה. צומת יקרא צאצא של x אם קיים מסלול מצומת x לצאצא (במסלול כל שני צמתים עוקבים מקיימים יחס אב-בן). שני צמתים יקראו אחים אם יש להם את אותו הורה. גובה של צומת - אורך המסלול (מספר צמתים) מהצומת ועד לעלה. גובה עץ - גובה של השורש. גודל העץ - מספר צמתיו. יתכן כי לצומת יהיה בן אחד בלבד. צומת מכילה נתונים ושני מצביעים: אחד לבן ימני והשני לבן שמאלי. מאחר וכל צומת הוא שורש של תת עץ - כל הפעולות על עצים הן רקורסיביות. ערכו של בן ימני יהיה גדול מערכו של צומת האב וערכו של צומת שמאלי קטן מערכו של צומת האב. לכן בהכנסת הנתונים נבדוק את הערך של הנתון שאנו מעוניינים להכניס לעץ - אם ערכו קטן מהשורש נפנה לבן השמאלי של השורש ואם לא נפנה לבן הימני של השורש. כשנפעיל פעולה כזו ברקורסיה נתייחס כעת לצומת החדש כשורש של תת העץ שהתקבל. נשווה את הערך שאנו מבקשים להכניס לעץ עם השורש - אם קטן נפנה לבנו השמאלי ואם לא נפנה לבנו הימיני וכך הלאה עד אשר נמצא את המיקם המתאים לערך שלנו. פעולות בסיסיות init - אתחול העץ. add, set - הכנסה לעץ. del - מחיקת העץ. תבנית של עץ:
כמו ברשימה יש מצביע לעץ שמכיל את הכתובת של שורש העץ, כל צומת בעץ מכיל את השדות של המבנה tree ושני מצביעים לבנים. הכנסת איבר לעץ ()add
הכנסת האיבר מתבצעת על ידי פונקציה רקורסיבית ()add. הפרמטרים שלה הם הערך שרוצים שהצומת (שמתפקדת בעץ כמו איברים שראינו ברשימות) תקבל (אם יש כמה כאלו יש לשלוח את הנתונים כפרמטרים לפונקציה ()add ) והפרמטר הנוסף - מצביע למצביע שמכיל את הכתובת של שורש העץ. בהכנסת איבר חדש יש להתאים את מקומו על פי הערך שרוצים להכניס לעץ (על פי התבנית שכל תת שורש מכיל בן שמאלי וימני כאשר הבן השמאלי מכיל ערך קטן מהשורש והבן הימני מכיל ערך גדול או שווה לשורש). כשמגיעים למקום המתאים, בונים צומת לפי הפונקציה set: הפונקציה set() מקבלת כתובת וערך, היא מקצה זיכרון לצומת החדש, מציבה את הערך המבוקש ומאתחלת את שני המצביעים של הצומת החדש ל- null - כלומר הצומת החדש הוא עלה, בעצם הפונקציה set בונה עלים לעץ. הצגת אברי העץ ()display
גם הצגת איברים מתבצעת על ידי פונקציה רקורסיבית הפועלת כך: לפונקציה נשלח האיבר הראשון של העץ. אם העץ לא ריק אז מציגים את תת עץ שמאלי - ניתן לראות זאת מכיוון שיש קריאה לפונקציה display() עם השורש של התת עץ השמאלי. לאחר שהגענו לעלה השמאלי ביותר מדפיסים את השדה הפשוט שלו (num), עולים לאב של העלה ואז יש שוב קריאה לפונקציה display() הפעם עם התת עץ הימני של הצומת שעליה דיברנו וכך הלאה עד שמגיעים לשורש העץ, מדפיסים את ערכו ושוב קוראים לפונקציה ()display עם תת העץ הימני של השורש. להלן תרשים של עץ, נראה איך הפונקציה ()display עוברת על צמתי העץ: המספרים בצמתים הם הערכים שהצמתים מכילים - ערך השדה הפשוט (במקרה זה - שדה מספרי) במבנה האיבר מסוג צומת של עץ (הם לא מציינים את סדר הטיפול בצמתים או סדר ההכנסה או כל משמעות אחרת). 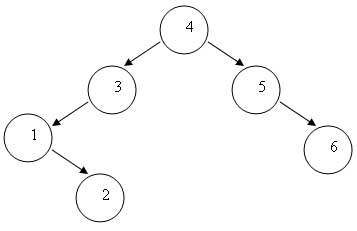
הצומת לא ריק לכן קוראים לפונקציה עם הצומת 3. צומת 3 לא ריק ולכן קוראים לפונקציה עם הצומת 1. הצומת 1 לא ריק ולכן קוראים לפונקציה עם null (הבן השמאלי של צומת 1 הוא null). הצומת ריק וחוזרים לקריאה הקודמת עם צומת 1, מדפיסים את ערכו וקוראים לפונקציה עם 2. הצומת לא ריק ולכן קוראים לפונקציה עם null (הבן השמאלי של צומת 1 הוא null). הצומת ריק וחוזרים לקריאה הקודמת עם צומת 2, מדפיסים את ערכו וקוראים לפונקציה עם null. הצומת ריק וחוזרים לקריאה הקודמת עם צומת 2, חוזרים לקריאה הקודמת עם צומת 1, חוזרים לקריאה הקודמת עם צומת 3, מדפיסים את ערכו וקוראים לפונקציה עם null (בנו הימיני של צומת 3). הצומת ריק וחוזרים לקריאה הקודמת עם צומת 3, חוזרים לקריאה הקודמת עם צומת 4, מדפיסים את ערכו, וקוראים לפונקציה עם צומת 5. הצומת לא ריק ולכן קוראים לפונקציה עם null (בנו השמאלי של 5). הצומת ריק ולכן חוזרים לקריאה הקודמת עם צומת 5, מדפיסים את ערכו וקוראים לפונקציה עם הצומת 6. הצומת לא ריק ולכן קוראים לפונקציה עם null (הבן השמאלי של צומת 6 ). הצומת ריק וחוזרים לקריאה הקודמת עם צומת 6, מדפיסים את ערכו וקוראים לפונקציה עם הצומת null (הבן הימיני של צומת 6). הצומת ריק וחוזרים לקריאה הקודמת עם צומת 6, חוזרים לקריאה הקודמת עם צומת 5, חוזרים לקריאה הקודמת עם צומת 4, לעותק הראשון והפונקציה מסיימת. נרשום רק את אשר הודפס למסך: צומת 1, צומת 2, צומת 3, צומת 4, צומת 5, צומת 6 - יש לשים לב כי פונקצית הדפסה זו מדפיסה את האיברים לפי סדר מהקטן לגדול. מחיקת העץ ()del_t
הפונקציה מקבלת את הכתובת של המצביע לשורש העץ. אם שורש העץ לא ריק קוראים לפונקציה עם הכתובת של השורש של תת העץ השמאלי, אם השורש של תת העץ השמאלי לא ריק שוב קוראים לפונקציה עם הכתובת של השורש של תת העץ של תת העץ של השורש של העץ וכך הלאה עד שמגיעים לעלה השמאלי ביותר. שני בניו הם null ולכן משחררים אותו על ידי פקודת delete. עולים בקריאות הרקורסיביות ושוב - אם תת העץ הימני לא ריק נכנסים לתת העץ הימני וכו' (התהליך של הקריאות הרקורסיביות דומה להצגת העץ בהבדל המזערי - רק לאחר שתי הקריאות הרקורסיביות מדפיסים את הכתובת ומשחררים את הזיכרון של הצומת). בסיום משחררים את שורש העץ. נרשום בקצרה על פי העץ שלנו מהתרשים באיזה סדר משתחררים הצמתים: צומת 2, צומת 1, צומת 3, צומת 6, צומת 5, צומת 4. נאחד את כל הפונקציות לתוכנית אחת:  דוגמא 1: דוגמא 1:
 העבר את העכבר מעל הדוגמא כדי לראות הסבר מפורט העבר את העכבר מעל הדוגמא כדי לראות הסבר מפורטעץ מלא - עץ שלכל צומת בו יש שני בנים. עץ שלם - עץ שבו לכל רמה i יש 2i צמתים.  דוגמא 2: דוגמא 2:
 העבר את העכבר מעל הדוגמא כדי לראות הסבר מפורט העבר את העכבר מעל הדוגמא כדי לראות הסבר מפורט הערה: הערה: כאשר אנו שולחים כארגומנט את העץ יש לשלוח עם אופרטור הכתובת על מנת שהשינויים של הוספה לעץ ומחיקתו ישמרו אך כפרמטר הפונקציה יש להשתמש במצביע למצביע כך שהמצביע מכיל משתנה מסוג מצביע (המצביע לעץ). כך לדוגמא אם המצביע לעץ מכיל את הכתובת 0a88 וכתובתו של מצביע זה היא fff4 אז המשתנה מצביע למצביע יהיה בכתובת מסוימת המכילה את הכתובת fff4 שתכיל את הכתובת של האיבר הראשון של העץ. כלומר מחוץ לפונקציות הנקראות:
מבחן 1. שורש העץ מכיל: (א) " ערכים פשוטים ומצביעים לשני בנים " מצביע לאיבר הראשון בעץ 2. אם הינו מחליפים בפונקצית ההדפסה בין פקודת ההדפסה לקריאה השנייה של הפונקציה הינו מקבלים את האיברים לפי הסדר: (ג) " כן, מהקטן לגדול " כן, מהגדול לקטן " לא 3. מה סדר הכנסת האיברים בעץ? (ב) " בכל צומת הבן הימני גדול מהאב " בכל צומת הבן השמאלי קטן מהאב והבן הימני גדול " בכל צומת הבן השמאלי קטן מהאב 4. איזו מבין הפונקציות הבאות לא רקורסיבית? (א) " Set() " Del_t() " Display() " Add()
|